


Next:1.2.4
Role of the ConstantUp:1.2
Complexity of AlgorithmsPrevious:1.2.2
Examples
1.2.3 An Example: Complexity
of Mergesort
Mergesort is a divide and conquer algorithm, as outlined
below. Note that the function mergesort calls itself recursively.
Let us try to determine the time complexity of this algorithm.
list mergesort (list L, int n);
{
if (n = = 1)
return (L)
else {
Split L into two halves L1 and L2 ;
return (merge (mergesort (L1,  ),
(mergesort (L2,
),
(mergesort (L2,  ))
))
}
}
Let T(n) be the running time of Mergesort on an input
list of size n. Then,
| T(n) |
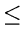 |
C1 (if n = 1)
(C1 is a constant) |
|
| |
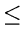 |
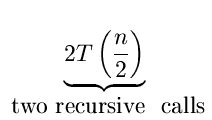 +
+ 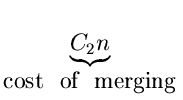 (if n > 1)
(if n > 1) |
|
If n = 2k for some
k, it can be shown that
T(n) 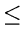 2kT(1) + C2k2k
That is, T(n) is O(nlog
n).
2kT(1) + C2k2k
That is, T(n) is O(nlog
n).
Figure 1.1: Growth rates of some functions
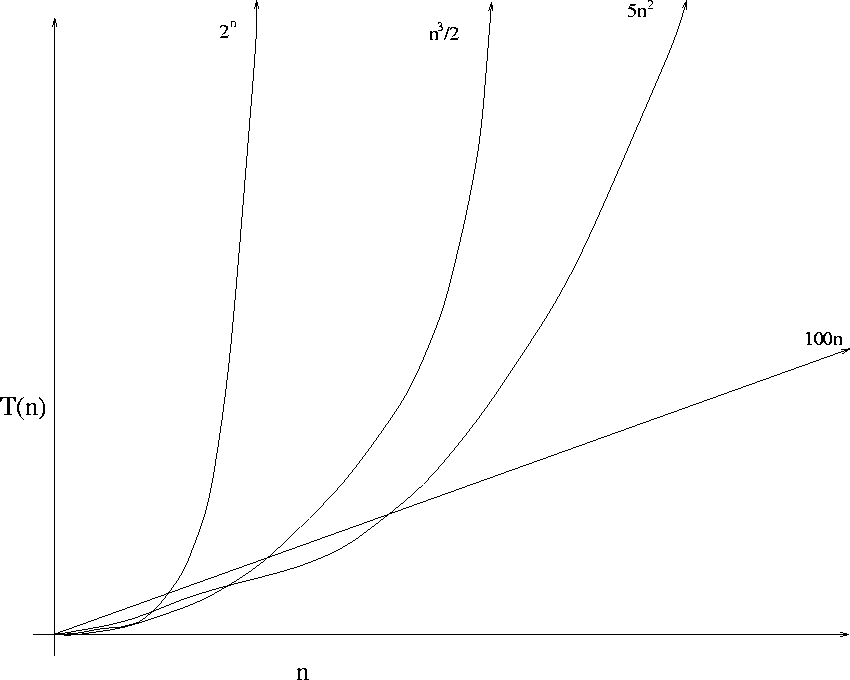 |
Table 1.1: Growth rate of functions
| |
Maximum Problem Size that can be solved in |
| T(n) |
100 |
1000 |
10000 |
| |
Time Units |
Time Units |
Time Units |
| |
|
|
|
| 100 n |
1 |
10 |
100 |
| |
|
|
|
| 5 n2 |
5 |
14 |
45 |
| |
|
|
|
| n3/2 |
7 |
12 |
27 |
| |
|
|
|
| 2n |
8 |
10 |
13 |
| |
|
|
|
|



Next:1.2.4
Role of the ConstantUp:1.2
Complexity of AlgorithmsPrevious:1.2.2
Examples
eEL,CSA_Dept,IISc,Bangalore
![]() ),
(mergesort (L2,
),
(mergesort (L2, ![]() ))
))
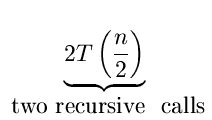 +
+ 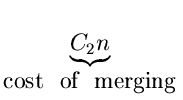 (if n > 1)
(if n > 1)