


Next:3.10
To Probe FurtherUp:3.9
Analysis of Skip ListsPrevious:3.9
Analysis of Skip Lists
3.9.1 Analysis of Expected Search
Cost
We analyze the search path backwards, traveling up and to the left. We
pretend as if the level of a node is being determined only when it is observed
while backtracking the search path.
-
1.
-
From level 1, we rise to level L(n)
-
2.
-
We move leftward
-
3.
-
We climb from L(n) to maxLevel.
At a particular point in the climb, we are at the ith
forward pointer of a node x and we have no knowledge about the levels
of nodes to the left of x or about the level of x (other
than that the level of x must be 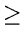 i
). See situation (a) in figure.
i
). See situation (a) in figure.
-
Assume ``x'' is not the header.
-
If level of x is i, then we are in situation (b).
If level of x is > i, we are in situation (c).
-
Prob{ we are in situation cA} = p
-
Each time we are in situation c, we climb up one level.
Let
| C(k) = |
expected length of a search path that |
| |
.climbs up k levels in an infinite list. |
Then:
| C(0) = |
0 |
| C(k) = |
p {cost in situation c } |
| |
(1 - p) { cost in situation b } |
We get
| C(k) = |
p {1 + C(k - 1)} + (1 - p){1
+ C(k)} |
| C(k) = |
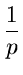 + C(k - 1)
+ C(k - 1) |
| C(k) = |
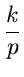 |
Our assumption that the list is infinite is pessimistic.
When we bump into the header in our backward climb, we simply climb
it up without performing any leftward (horizontal) movements.
This gives us an upperbound of
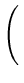
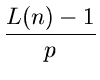
 On the expected length of a path that climbs up from level 1 to level
L(n)
in a list of n elements. (because L(n) - 1 level are
being climbed).
On the expected length of a path that climbs up from level 1 to level
L(n)
in a list of n elements. (because L(n) - 1 level are
being climbed).
The rest of the journey includes
-
1.
-
leftward movements, the number of which is bounded by the number of elements
of level L(n)or higher. his has an expected value =
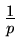
-
2.
-
We also move upwards from level L(n) to the maximum level
in the list.
| p { maximum level in the list |
> k} |
| |
= 1 - (1 - pk)n |
| |
 npk npk |
p { 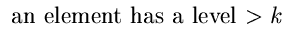 } } |
= pk |
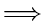 p
{ p
{ 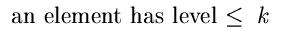 } } |
= 1 - pk |
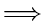 p
{ p
{ 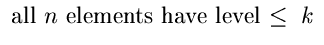 } } |
= (1 - pk)n |
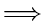 p
{ p
{ 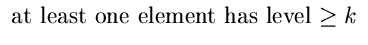 } } |
= 1 - (1 - pk)n |
| Expected maximum level |
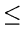 npk npk |
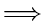 Expected maximum level
Expected maximum level |
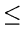 L(n)
+ L(n)
+ 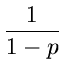 |
Putting our results together, we get:
Total expected cost to climb out of a list on n elements
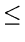
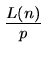 +
+ 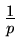 which is O(log n).
which is O(log n).
We can also compute the probability if the actual cost of a search exceeds
expected cost by more than a specified ratio.
Examples
-
1.
-
p =
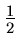 ;
n = 256
;
n = 256
p
{search will take longer than 3 times the expected cost } = 
-
2.
-
p =
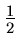 ;
n = 4096
;
n = 4096
p
{search will take longer than 2 times the expected cost } = 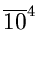
-
3.
-
p =
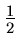 ;
n = 1024
;
n = 1024
p
{search will take longer than 3 times } = 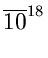
How do we choose p ?
-
Decreasing p increases variability of running times.
-
p =
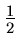 ; generation of random level can be done from a stream of random bits.
; generation of random level can be done from a stream of random bits.
-
Decreasing p decreases # of pointers per node.
-
Overheads are related to L(n) rather than
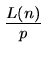 .
.
-
p =
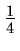 is probably the best choice, unless variability of running times is an
issue.
is probably the best choice, unless variability of running times is an
issue.



Next:3.10
To Probe FurtherUp:3.9
Analysis of Skip ListsPrevious:3.9
Analysis of Skip Lists
eEL,CSA_Dept,IISc,Bangalore
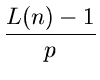
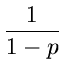
![]()
![]() +
+ ![]() which is O(log n).
which is O(log n).