1.2.1 Big Oh Notation

-

A convenient way of describing the growth rate of a function and hence the time complexity of an algorithm.

Let n be the size of the input and f (n), g(n) be positive functions of n.

DEF.Big Oh. f (n) is O(g(n)) if and only if there exists a real, positive constant Cand a positive integer n₀ such that

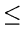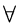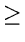f (n) $$\leq$$Cg(n) $$\forall$$   n$$\geq$$n₀

• Note that O(g(n)) is a class of functions.
• The "Oh" notation specifies asymptotic upper bounds
• O(1) refers to constant time. O(n) indicates linear time; O(n^k) (k fixed) refers to polynomial time; O(log n) is called logarithmic time; O(2ⁿ) refers to exponential time, etc.