3.6.1 Result 1: Unsuccessful Search

 $\mbox{$\bullet$}$

The expected number of probes in an unsuccessful search $\leq$${\frac{1}{1 -\alpha}}$

Proof: In an unsuccessful search, every probe but the last accesses an occupied slot that does not contain the desired key and the last slot probed is empty.

 

 
 
 

Let the random variable X denote the number of occupied slots probed before hitting an empty slot. X can take values 0, 1,..., n. It is easy to see that the expected number of probes in an unsuccessful search is 1 + E[X].

$$\mbox{ exactly $i$\space probes access occupied slots}$$ p_i =

for i > n, p_i = 0 since we can find at most n occupied slots.

Thus the expected number of probes 
                                                        = 1 + $$\sum_{i=0}^{n}$$ip_i                                                 (*)
To evaluate (*), define 

                   q_i = P{at least  i  probes access occupied slots}
and use the identity: 
                $$\sum_{i=0}^{n}$$ip_i = $$\sum_{i=1}^{n}$$q_i
To compute q_i, we proceed as follows: 
                                        q₁ = $${\frac{n}{m}}$$
since the probability that the first probe accesses an occupied slot is n/m.

With uniform hashing, a second probe, if necessary, is to one of the remaining m - 1 unprobed slots, n - 1 of which are occupied. Thus 
                                        q₂ = $$\left(\vphantom{\frac{n}{m}}\right.$$$${\frac{n}{m}}$$$$\left.\vphantom{\frac{n}{m}}\right)$$$$\left(\vphantom{\frac{n-1}{m-1}}\right.$$$${\frac{n-1}{m-1}}$$$$\left.\vphantom{\frac{n-1}{m-1}}\right)$$
since we make a second probe only if the first probe accesses an occupied slot.

In general,

$$\left(\vphantom{\frac{n}{m}}\right. {\frac{n}{m}} \left.\vphantom{\frac{n}{m}}\right) \left(\vphantom{\frac{n-1}{m-1}}\right. {\frac{n-1}{m-1}} \left.\vphantom{\frac{n-1}{m-1}}\right) \left(\vphantom{\frac{n-i+1}{m-i+1}}\right. {\frac{n-i+1}{m-i+1}} \left.\vphantom{\frac{n-i+1}{m-i+1}}\right)$$ q_i =

$$\leq \left(\vphantom{\frac{n}{m}}\right. {\frac{n}{m}} \left.\vphantom{\frac{n}{m}}\right)^{i{_}}_{} \alpha^{i}_{} {\frac{n-j}{m-j}} \leq {\frac{n}{m}}$$

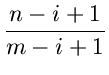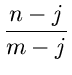Thus the expected number of probes in an unsuccessful search

$$\sum_{i=o}^{n}$$ =

$$\leq \alpha \alpha^{2}_{}$$

$${\frac{1}{1 -\alpha}}$$ =

 $\mbox{$\bullet$}$

Intuitive Interpretation of the above:

 

 
 
 

One probe is always made, with probability approximately $\alpha$ a second probe is needed, with probability approximately $\alpha^{2}_{}$ a third probe is needed, and so on.