10.7 Problems

1.

Show that an algorithm that makes at most a constant number of calls to polynomial-time subroutines runs in polynomial time, but that a polynomial number of calls to polynomial-time subroutines may result in an exponential-time algorithm.

2.

A Hamiltonian path in a graph is a simple path that visits every vertex exactly once. Show that the decision problem of determining whether or not there is a Hamiltonian path from a given vertex u to another given vertex v belongs to NP

3.

Show that the 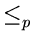$\leq_{p}^{}$ relation is a transitive relation on the set of problems.

4.

Given an undirected graph, the Hamiltonian cycle problem determines whether a graph has a Hamiltonian cycle. Given that the Hamiltonian cycle problem for undirected graphs is NP-Complete, what can you say about the Hamiltonian cycle problem for directed graphs? Provide reasons for your answer.