


Next:10.6
To Probe FurtherUp:10.5
NP-Complete ProblemsPrevious:10.5
NP-Complete Problems
10.5.1 NP-Hardness and NP-Completeness
A decision problem Y is said to be NP-hard if X 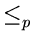 Y
Y 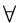 X
X  NP. An NP-hard problem Y is said to be NP-complete if Y
NP. An NP-hard problem Y is said to be NP-complete if Y  NP.
NPC is the standard notation for the class of all NP-complete problems.
NP.
NPC is the standard notation for the class of all NP-complete problems.
-
Informally, an NP-hard problem is a problem that is at least as hard as
any problem in NP. If, further, the problem also belongs to NP,
it would become NP-complete.
-
It can be easily proved that if any NP-complete problem is in P,
then NP = P. Similarly, if any problem in NP is not
polynomial-time solvable, then no NP-complete problem will be polynomial-time
solvable. Thus NP-completeness is at the crux of deciding whether or not
NP = P.
-
Using the above definition of NP-completeness to show that a given decision
problem, say Y, is NP-complete will call for proving polynomial reducibility
of each problem in NP to the problem Y. This is impractical since
the class NP already has a large number of member problems and will
continuously grow as researchers discover new members of NP.
-
A more practical way of proving NP-completeness of a decision problem
Y is to discover a problem X
 NPC
such that X
NPC
such that X 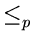 Y. Since X is NP-complete and
Y. Since X is NP-complete and 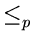 is a transitive relationship, the above would mean that Z
is a transitive relationship, the above would mean that Z 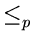 Y
Y 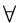 Z
Z  NP.
Furthermore if Y
NP.
Furthermore if Y  NP,
then Y is NP-complete.
NP,
then Y is NP-complete.
The above is the standard technique used for showing the NP-hardness
or NP-completeness of a given decision problem. For example, all the decision
problems given in Section 10.2 can be shown to be NP-complete by the above
technique.
-
An interesting question is: how was the first member of NPC found?
Stephen Cook showed the NP-completeness of the problem 3-SAT by directly
proving that X
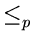 3-SAT
3-SAT 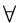 X
X  NP.
NP.
-
If a problem is NP-complete, it does not mean that all hopes are lost.
If the actual input sizes are small, an algorithm with, say, exponential
running time may be acceptable. On the other hand, it may still be possible
to obtain near-optimal solutions in polynomial-time. Such an algorithm
that returns near-optimal solutions (in polynomial time) is called an approximation
algorithm. Using Kruskal's algorithm to obtain a suboptimal solution to
the TSP (see Chapter 8) is an example of this.



Next:10.6
To Probe FurtherUp:10.5
NP-Complete ProblemsPrevious:10.5
NP-Complete Problems
eEL,CSA_Dept,IISc,Bangalore