


Next:10.4
The Classes P and NPUp:10.3
Examples of some Intractable ProblemsPrevious:10.3.5
Job Shop Scheduling
10.3.6 Satisfiability
A propositional variable is one that can be assigned the value
true or
false. A literal is a propositional variable or its negation. A clause
is a sequence of literals separated by the logical OR operator. A propositional
formula is said to be in conjunctive normal form (CNF) if it consists of
a sequence of clauses separated by the logical AND operator. For example,
(p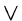 q
q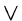 s)
s)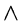 (
(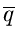
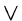 r)
r)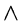 (
(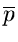
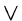
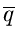
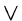 r
r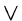
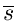 )
)
A truth assignment for a set of propositional variables is an assignment
of true or false value to each propositional variable. A truth assignment
is said to satisfy a formula if it makes the value of the formula true.
3-SAT (Decision Problem): Given a CNF formula in which each clause is
permitted to contain at most three literals, is there a truth assignment
to its variables that satisfies it?
eEL,CSA_Dept,IISc,Bangalore
![]() q
q![]() s)
s)![]() (
(![]()
![]() r)
r)![]() (
(![]()
![]()
![]()
![]() r
r![]()
![]() )
)