


Next: 8.7.2 Traveling Salesman Problem
Up: 8.7 Programming Assignments
Previous: 8.7 Programming Assignments
This assignment involves five problems.
- 1.
- Generate a connected graph with n vertices and
a certain number of edges, decided by an average degree
d of each vertex. The connected graph generated should
have several spanning trees and several
Hamiltonian paths. Also, generate random costs
for all the edges.
- 2.
- Find a minimum cost spanning tree (MST) for the above
graph, using an efficient implementation of Prim's algorithm.
Compute the execution time of this program.
- 3.
- Find an MST using Kruskal's algorithm. In the implementation,
use the heap data structure to organize the set of edges
and the MFSET data structure to implement union's
and find's. Compare the execution time with that of Prim's
algorithm.
- 4.
- Find a second best MST by extending the Kruskal's
algorithm, using the following property: If T is an MST,
then there exist an edge
(u, v)
 T and an edge
(x, y)
T and an edge
(x, y) 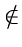 T such that
(T - {(u, v)})U{(x, y)} is a second best MST.
T such that
(T - {(u, v)})U{(x, y)} is a second best MST.
- 5.
- Find a Hamiltonian path using a greedy strategy
based on Kruskal's algorithm. You can compare the
cost of this path to that of a minimal cost Hamiltonian
path (found by exhaustive enumeration) for values of
n up to 10. In fact, you can do a little better
by using the branch and bound method to
compute the minimal cost Hamiltonian path.
- 6.
- Provide examples of connected graphs for situations specified below. If an example
cannot exist for the situation, provide reasons.
- (a)
- A graph in which a maximum cost edge is a part of every
MST in the graph
- (b)
- A graph in which a maximum cost edge is never a part of
any MST
- (c)
- A graph in which a least cost edge is not a part of any
MST
- 7.
- Let T be a minimum spanning tree of a connected graph G.
Prove that there exist edges
(u, v)
 T and
(x, y)
T and
(x, y) 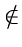 Tsuch that
T - {(u, v)}
Tsuch that
T - {(u, v)} 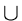 {(x, y)} is a second-best
minimum spanning tree of G.
{(x, y)} is a second-best
minimum spanning tree of G.



Next: 8.7.2 Traveling Salesman Problem
Up: 8.7 Programming Assignments
Previous: 8.7 Programming Assignments
eEL,CSA_Dept,IISc,Bangalore