


Next: 8.7 Programming Assignments
Up: 8. Undirected Graphs
Previous: 8.5 To Probe Further
- 1.
- Consider an undirected graph G=(V, E), with n vertices.
Show how a one dimensional array of length
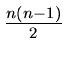 can be used to represent G.
can be used to represent G.
- 2.
- Give an algorithm that determines whether or not a given undirected
graph
G = (V, E) contains a cycle. The algorithm should run in
O(|V|) time independent of |E|.
- 3.
- Design an algorithm to enumerate all simple cycles of a graph. How many
such cycles can there be? What is the time complexity of the algorithm?
- 4.
- Let (u, v) be a minimum-weight edge in a graph G. Show that
(u, v) belongs to some minimum spanning tree of G.
- 5.
- Let e be maximum-weight edge on some cycle of G = (V, E). Prove
that there is a minimum spanning tree of
G
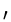 = (V, E - {e}) that
is also a minimum spanning tree of G.
= (V, E - {e}) that
is also a minimum spanning tree of G.
- 6.
- For an undirected graph G with n vertices and e edges,
show that
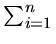 di = 2e where di is the
degree of vertex i (number of edges incident on vertex i).
di = 2e where di is the
degree of vertex i (number of edges incident on vertex i).
- 7.
- The diameter of a tree T = (V, E) is defined by
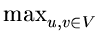
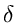 (u, v) where
(u, v) where
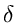 (u, v) is the shortest-path distance from vertex u
to vertex v. Give
an efficient algorithm to compute the diameter of a tree, and analyze the
running time of the algorithm.
(u, v) is the shortest-path distance from vertex u
to vertex v. Give
an efficient algorithm to compute the diameter of a tree, and analyze the
running time of the algorithm.
- 8.
- An Eulerian walk in an undirected graph is a path
that starts and ends at the same vertex, traversing every edge
in the graph exactly once. Prove that in order for such a path
to exist, all nodes must have even degree.
- 9.
- Two binary trees T1 and T2 are said to be isomorphic
if T1 can be transformed into T2 by swapping left and right
children of (some of the) nodes in T1. Design an efficient
algorithm to decide id two given trees are isomorphic. What is
the time complexity of your algorithm?



Next: 8.7 Programming Assignments
Up: 8. Undirected Graphs
Previous: 8.5 To Probe Further
eEL,CSA_Dept,IISc,Bangalore
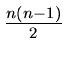 can be used to represent G.
can be used to represent G.
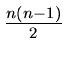 can be used to represent G.
can be used to represent G.