7.7 Problems

1.

Give a simple example of a directed graph with negative-weight edges for which Dijkstra's algorithm produces incorrect answers. Why doesn't the proof of Dijkstra's algorithm go through when negative-weight edges are allowed?

2.

Give an example of a four node directed graph with some negative-weight edges for which Dijkstra's algorithm produces incorrect answers. Also, give an example of a four node directed graph with some negative-weight edges for which Dijkstra's algorithm always produces correct answers. In either case, justify your answer.

3.

Explain how to modify Dijkstra's algorithm so that if there is more than one minimum path from source to a destination vertex, then a path with the fewest number of edges is chosen.

4.

Suppose that in implementing Dijkstra's shortest path algorithm, one uses an AVL tree rather than a partially ordered tree for representing the dynamic set of non-special vertices. What will be the worst case complexity of the algorithm if an adjacency list representation is used for the digraph? Would you still prefer the partially ordered tree implementation?

5.

We are given a directed graph G = (V, E) on which each edge (u, v) $\in$ E has an associated value r(u, v), which is a real number in the range 0 $\leq$ r(u, v) $\leq$ 1 that represents the reliability of a communication channel from vertex u to vertex v. We interpret r(u, v)as the probability that the channel from u to v will not fail, and we assume that these probabilities are independent. Give an efficient algorithm to find the most reliable path between two vertices.

6.

Write a program to find the longest path in a directed acyclic graph. What is the complexity of the algorithm?

7.

Describe a mathematical model for the following scheduling problem: Given tasks T₁, T₂,..., T_n, which require time t₁, t₂,..., t_n to complete, and a set of constraints, each of the form T_j must be completed prior to the start of T_i, find the minimum time necessary to complete all the tasks assuming unlimited number of processors to be available.

8.

In a depth-first search of a directed graph G = (V, E), define d (v) as the timestamp when v is visited for the first time and f (v)the timestamp when the search finishes examining the adjacency list of v. Show that an edge (u, v) $\in$ E is

(a)

a tree edge or forward edge if and only if d[u] < d[v] < f[v] < f[u].

(b)

a back edge if and only if d[v] < d[u] < f[u] < f[v].

(c)

a cross edge if and only if d[v] < f[v] < d[u] < f[u].

9.

An Euler Tour of a connected, directed graph G = (V, E) is a cycle that traverses each edge of G exactly once, although it may visit a vertex more than once.

(a)

Show that G has an Euler tour if and only if indegree(v) = outdegree(v) 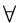$\forall$v $\in$ V.

(b)

Describe an O(e) algorithm to find an Euler tour of G if one exists, where e is the number of edges.

10.

Design an efficient algorithm to determine whether a given DAG is a tree.

11.

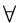Let G= (V, E) be a digraph. Define a relation R on V such that uRv if and only if u and v lie on a common (not necessarily simple) cycle. Prove that R is an equivalence relation on V.