7.5.1 Test for Acyclicity

Result:

A digraph is acyclic if and only if its first search does not have back arcs.

Proof:

First we prove that

backarc 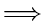$\Longrightarrow$ cycle.

Let (u 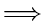$\Longrightarrow$w) be a backarc. This means that w is an ancestor of v. Thus (w,..., v, w) will be a cycle in the digraph.

Next we show that

cycle 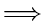$\Longrightarrow$ backarc.

Suppose G is cyclic. Consider a cycle and let v be the vertex with the lowest dfnumber on the cycle. See Figure 7.13. Because v is on a cycle, there is a vertex u such that (u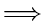$\Longrightarrow$v) is an edge. Since v has the lowest dfnumber among all vertices on the cycle, umust be an descendant of v.

• it can not be a tree arc since dfnumber(v) 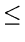$\leq$dfnumber(u)
• it can not be a forward arc for the same reason
• it can not be a cross arc since v and u are on the same cycle.

Note that the above test for acyclicity has worst case complexity O(e).