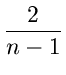Next:2.
ListsUp:1.
IntroductionPrevious:1.3
To Probe Further
1.4 Problems
-
1.
-
Assuming that n is a power of 2, express the output of the following
program in terms of n.
int mystery (int n)
{ int x=2, count=0;
while (x < n) { x *=2; count++}
return count;
}
-
2.
-
Show that the following statements are true:
-
(a)
-
 is O(n2)
is O(n2)
-
(b)
-
max(n3, 10n2)
is O(n3)
-
(c)
-
 ik
is O(nk + 1) and
ik
is O(nk + 1) and  (nk
+ 1), for integer k
(nk
+ 1), for integer k
-
(d)
-
If p(x) is any kth degree polynomial with
a positive leading coefficient, then p(n) is O(nk)
and
 (nk).
(nk).
-
3.
-
Which function grows faster?
-
(a)
-
nlog n; (logn)n
-
(b)
-
lognk; (logn)k
-
(c)
-
nlogloglog n; (log
n)!
-
(d)
-
nn; n!.
-
4.
-
If f1(n) is O(g1(n))
and f2(n) is O(g2(n))
where f1and f2 are positive functions
of n, show that the function f1(n)
+ f2(n) is O(max(g1(n),
g2(n))).
-
5.
-
If f1(n) is O(g1(n))
and f2(n) is O(g2(n))
where f1and f2 are positive functions
of n, state whether each statement below is true or false. If the
statement is true(false), give a proof(counter-example).
-
(a)
-
The function | f1(n)
- f2(n)| is O(min(g1(n),
g2(n))).
-
(b)
-
The function | f1(n)
- f2(n)| is O(max(g1(n),
g2(n))).
-
6.
-
Prove or disprove: If f (n) is a positive function of n,
then f (n) is O(f
(
 )).
)).
-
7.
-
The running times of an algorithm A and a competing algorithm A'
are described by the recurrences
-
T(n) = 3T(
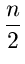 )
+ n; T'(n)
= aT'(
)
+ n; T'(n)
= aT'( )
+ n
)
+ n
respectively. Assuming T(1)
= T'(1) = 1, and n = 4k for some positive
integer k, determine the values of a for which A'
is asymptotically faster than A.
-
8.
-
Solve the following recurrences, where T(1) = 1 and T(n)
for n
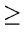 2 satisfies:
2 satisfies:
-
(a)
-
T(n) = 3T(
 )
+ n
)
+ n
-
(b)
-
T(n) = 3T(
 )
+ n2
)
+ n2
-
(c)
-
T(n) = 3T(
 )
+ n3
)
+ n3
-
(d)
-
T(n) = 4T(
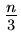 )
+ n
)
+ n
-
(e)
-
T(n) = 4T(
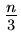 )
+ n2
)
+ n2
-
(f)
-
T(n) = 4T(
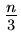 )
+ n3
)
+ n3
-
(g)
-
T(n) = T(
 )
+ 1
)
+ 1
-
(h)
-
T(n) = 2T(
 )
+ log n
)
+ log n
-
(i)
-
T(n) = 2T(
 )
+ n2
)
+ n2
-
(j)
-
T(n) = 2T(n
- 1) + 1
-
(k)
-
T(n) = 2T(n
- 1) + n
-
9.
-
Show that the function T(n) defined by T(1) = 1 and
-
T(n) = T(n - 1) +
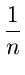
for n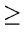 2 has the complexity O(log n).
2 has the complexity O(log n).
-
10.
-
Prove or disprove: f(3**n) is O(f(2**n))
-
11.
-
Solve the following recurrence relation:
-
T(n)
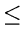 cn
+
cn
+ 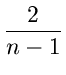
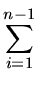 T(i)
T(i)
where c is a constant, n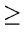 2, and T(2) is known to be a constant c1.
2, and T(2) is known to be a constant c1.



Next:2.
ListsUp:1.
IntroductionPrevious:1.3
To Probe Further
eEL,CSA_Dept,IISc,Bangalore
 is O(n2)
is O(n2) ik
is O(nk + 1) and
ik
is O(nk + 1) and  (nk
+ 1), for integer k
(nk
+ 1), for integer k (nk).
(nk). )
+ n
)
+ n )
+ n2
)
+ n2 )
+ n3
)
+ n3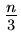 )
+ n
)
+ n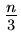 )
+ n2
)
+ n2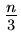 )
+ n3
)
+ n3 )
+ 1
)
+ 1 )
+ log n
)
+ log n )
+ n2
)
+ n2