- Insert r into L in the proper order.
- Note that no modifications are necessary to the ancestors of L.
- request the file system for a new block L' and move the last half of
the records from L to L', inserting r into its proper place in L or
L'.
Let
P = parent of L (5.9) k' = smallest key value in L' (5.10) 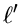
= pointer to L'
Insert k' and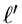 in P (recursively)
in P (recursively)
- If P already has m pointers, insertion of k' and
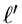 into P will cause P to be split and will necessitate an insertion of a key
and a pointer in the parent of P.
into P will cause P to be split and will necessitate an insertion of a key
and a pointer in the parent of P.
- The recursive scheme can ripple all the way up to the root causing
the root to be split, in which case
- Create a new root with the two halves of the old root as its two
children. This
- increases the number of levels
- is the only situation where a node has fewer
than
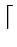 m/2
m/2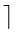 children.
children.
- Create a new root with the two halves of the old root as its two
children. This